|
|
Programmer ASP.NET MVC C# |
Others
|
|||||||||||||||||||||
| Previous | Next | ||||||||||||||||||||
|
Парадокс дней рождения — утверждение, что если дана группа из 23 или более человек, то вероятность того, что хотя бы у двух из них дни рождения (число и месяц) совпадут, превышает 50 %. Для группы из 60 или более человек вероятность совпадения дней рождения хотя бы у двух её членов составляет более 99 %, хотя 100 % она достигает, только когда в группе не менее 366 человек (с учётом високосных лет — 367). Такое утверждение может показаться противоречащим здравому смыслу, так как вероятность одному родиться в определённый день года довольно мала, а вероятность того, что двое родились в конкретный день — ещё меньше, но является верным в соответствии с теорией вероятностей. Таким образом, оно не является парадоксом в строгом научном смысле — логического противоречия в нём нет, а парадокс заключается лишь в различиях между интуитивным восприятием ситуации человеком и результатами математического расчёта. Интуитивное восприятие Один из способов понять на интуитивном уровне, почему в группе из 23 человек вероятность совпадения дней рождения у двух человек столь высока, состоит в осознании следующего факта: поскольку рассматривается вероятность совпадения дней рождения у любых двух человек в группе, то эта вероятность определяется количеством пар людей, которые можно составить из 23 человек. Так как порядок людей в парах не имеет значения, то общее число таких пар равно числу сочетаний из 23 по 2, то есть 23 х 22/2 = 253 пары. Посмотрев на это число, легко понять, что при рассмотрении 253 пар людей вероятность совпадения дней рождения хотя бы у одной пары будет достаточно высокой. Ключевым моментом здесь является то, что утверждение парадокса дней рождения говорит именно о совпадении дней рождения у каких-либо двух членов группы. Одно из распространённых заблуждений состоит в том, что этот случай путают с другим — похожим, на первый взгляд, — случаем, когда из группы выбирается один человек и оценивается вероятность того, что у кого-либо из других членов группы день рождения совпадёт с днем рождения выбранного человека. В последнем случае вероятность совпадения значительно ниже. Расчёт вероятности В данном примере для расчёта вероятности того, что в группе из n человек как минимум у двух дни рождения совпадут, примем, что дни рождения распределены равномерно, то есть нет високосных лет, близнецов, рождаемость не зависит от дня недели, времени года и других факторов. В действительности, это не совсем так — обычно летом рождается больше детей; кроме того, в некоторых странах из-за особенностей работы больниц больше детей рождается в определённые дни недели. Однако неравномерность распределения может лишь увеличить вероятность совпадения дней рождения, но не уменьшить: если бы все люди рождались только в 3 дня из 365, то вероятность совпадения дней рождения была бы очень высокой. Рассчитаем сначала, какова вероятность p (n) того, что в группе из n человек дни рождения всех людей будут различными. Если n > 365, то в силу принципа Дирихле вероятность равна нулю. Если же n ? 365, то будем рассуждать следующим образом. Возьмём наугад одного человека из группы и запомним его день рождения. Затем возьмём наугад второго человека, при этом вероятность того, что у него день рождения не совпадёт с днем рождения первого человека, равна 1 — 1/365. Затем возьмём третьего человека, при этом вероятность того, что его день рождения не совпадёт с днями рождения первых двух, равна 1 — 2/365. Рассуждая по аналогии, мы дойдём до последнего человека, для которого вероятность несовпадения его дня рождения со всеми предыдущими будет равна 1 — (n — 1)/365. Перемножая все эти вероятности, получаем вероятность того, что все дни рождения в группе будут различными:
Тогда вероятность того, что хотя бы у двух человек из n дни рождения совпадут, равна
Значение этой функции превосходит 1/2 при n = 23 (при этом вероятность совпадения равна примерно 50.7 %). Вероятности для некоторых значений n иллюстрируются следущей таблицей:
|
|||||||||||||||||||||



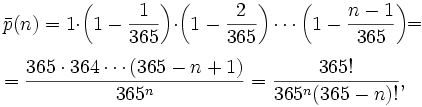
Мистер Смит сообщает, что у него двое детей и по крайней мере один из них мальчик. Какова вероятность того, что второй ребенок мистера Смита тоже мальчик? Первое, что приходит в голову, — это сказать, что вероятность равна 1/2, но, перебрав три равновероятных возможности — ММ, МД, ДМ, — мы видим, что ММ — только одна из них, следовательно, искомая вероятность равна 1/3 [Если дети не близнецы!]. Ситуация резко изменилась бы, если бы Смит сказал, что мальчиком является старший (или тот, кто повыше ростом, или тот, чей вес больше) из его детей. В этом случае допустимые комбинации исчерпываются двумя — ММ и МД — и вероятность того, что другой ребенок мистера Смита мальчик, возрастает до 1/2.